Derive PCA from Gaussian Ellipse

Principle component analysis (PCA) is a fundamental tool for dimension reduction. It’s operations is quite simple: center the data, calculate the covariance matrix, perform eigenvalue decomposition and these eigenvector are “principle components”, which is also called eigenface if the data is face images.

However, the proof of PCA is complicated for beginners. Here I want to derive PCA from the Gaussian distribution, so that readers can get intuition on how PCA works.

Suppose we draw a dataset $X={x_1,x_2,…,x_n}$ from a Gaussian distribution $\mathcal{N}(0, \Sigma)$ in $\mathcal{R}^2$, as show in figure below:

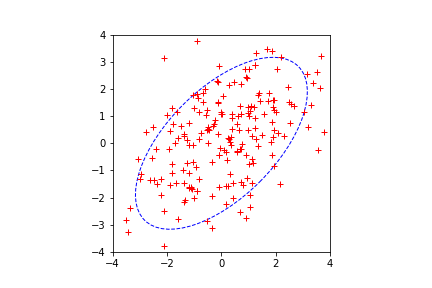
Our goal is to find the best projection subspace, i.e. if we project data onto it, we get minimal reconstruction error:

$s$ is the subspace, $x_i^s$ is $x_i$’s projection onto $s$.

Clearly, the long axis of the ellipse is the ideal subspace. The ellipse is defined as: $x^\top \Sigma^{-1} x = r^2$, $r$ is a constant. From eigenvalue decomposition $\Sigma = \Phi ^\top \Lambda \Phi $, $\Sigma^{-1} = \Phi ^\top \Lambda^{-1} \Phi $, $\Lambda = diag(\sigma_{\max},\sigma_{\min})$. Thus we can rewrite the left hand side of ellipse equation:

From Rayleigh quotient, $\sigma_{\max}^{-1} \leq \frac{x^{\top}}{\left | x \right |} \Phi^{\top} \Lambda^{-1} \Phi \frac{x}{\left | x \right |} \leq \sigma_{\min}^{-1}$, when $\frac{x}{\left | x \right |}$ is corresponding eigenvector. Thus $\left | x \right |^2 = \sigma_{\max} r^2$ when the point direction is the largest eigenvector, $\left | x \right |^2 = \sigma_{\min} r^2$ when the point direction is the smallest eigenvector. It suggests that the eigenvectors are actually the axes of ellipse, and the axis length is propotional to eigenvalue.

In summary, the best subspace is the largest eigenvector. This is exactly what PCA does!