EM Algorithm Convergence Proof with KL Divergence

EM algorithm Convergence Proof with KL Divergence

In my previous blog, I introduce the derivation of EM algorithm and convergence proof via defining its auxiliary function. Here I will introduce another method to prove the convergence of EM.

First let us denote $X, Z$ as the observed variable and hidden variable, and denote $D$ as collected iid samples, $\theta$ as the parameters.

$\begin{aligned} P_{X,Z}(D,z;\theta)&=P_{Z|X}(z|D;\theta)P_X(D;\theta) \\ \log P_X(D;\theta)&=\log P_{X,Z}(D,z;\theta)-\log P_{Z|X}(z|D;\theta) \end{aligned}$

Taking expectations on both sides and using the fact that the left hand side does not depend on Z.

$\begin{aligned} \log P_X(D;\theta)&=E_{Z|X;\theta^n}(\log P_{X,Z}(D,z;\theta))-E_{Z|X;\theta^n}(\log P_{Z|X}(z|D;\theta)) \\ &=Q(\theta,\theta^n)+H(\theta,\theta^n) \end{aligned}$
where Q function is what EM algorithm actually optimize, and Q is the lower bound of log likelihood. Note that:

$\begin{aligned} H(\theta,\theta^n)&=-E_{Z|X;\theta^n}(\log P_{Z|X}(z|D;\theta)) \\ &=-\int P_{Z|X}(z|D;\theta^n) \log P_{Z|X}(z|D;\theta) dz \\ &=-\int p_n(z) \log p(z) dz \\ &=KL[p_n||p]+H[p_n] \end{aligned}$
where $KL[p||q]$ is the Kullback-Leibler divergence between $p$ and $q$, and $H[p]$ the entropy of $p$ itself. So $H(\theta,\theta^n) \geq 0, \log P_X(D;\theta) \geq H(\theta,\theta^n)$

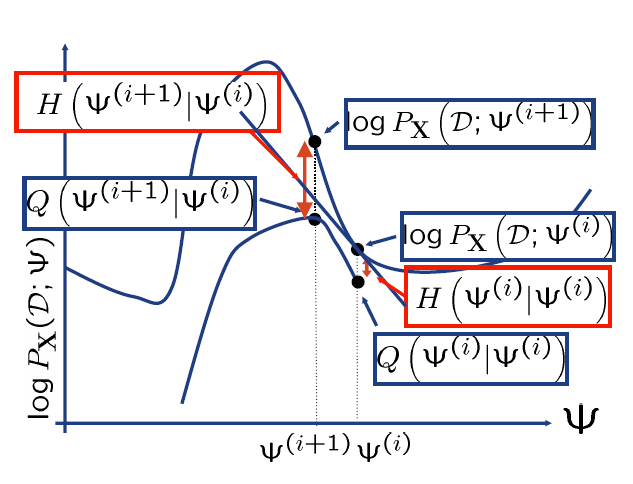
To prove the convergence of EM, we need to prove:

$\begin{aligned} &\log P_X(D;\theta^{n+1}) \geq \log P_X(D;\theta^n) \\ &\log P_X(D;\theta^{n+1}) - \log P_X(D;\theta^n) \\ &=Q(\theta^{n+1},\theta^n)+H(\theta^{n+1},\theta^{n})-Q(\theta^{n},\theta^n)-H(\theta^{n},\theta^{n}) \\ &=Q(\theta^{n+1},\theta^n)-Q(\theta^{n},\theta^n)+KL[p_n||p_{n+1}]+H[p_n]-KL[p_n||p_n]-H[p_n] \\ &=Q(\theta^{n+1},\theta^n)-Q(\theta^{n},\theta^n)+KL[p_n||p_{n+1}] \end{aligned}$
In M step we optimize $Q, Q(\theta^{n+1},\theta^n)\geq Q(\theta^{n},\theta^n)$, so $\log P_X(D;\theta^{n+1}) - \log P_X(D;\theta^n)$. The convergence of EM is proved, but note that there is no guarantee of convergence to global maximum.

And since in the proof, we just increase Q function rather than maximize it. So in M step any step that increases it is sufficient, it is very useful when M-step is itself non-trivial:
* e.g. if there is no closed-form solution one has to resort to numerical methods, like gradient ascent.
* can be computationally intensive, lots of iterations per M-step
* in these cases, it is usually better to just perform a few iterations and move on to the next E-step
* no point in precisely optimizing M-step if everything is going to change when we compute the new E-step

Derive the Form of Discrete Variables

In previous part, I have derived the following form of Q function.

$Q(\theta,\theta^n)={\sum_{t=1}^{T}}{\sum_{i=0}^{C}}P(Z=i|X=x_t;\theta^n) \log{P(X=x_t,Z=i;\theta)}$

Next I will show how to derive it from the Q function above.

$E_{Z \sim P(z|D;\theta^n)}(\log P_{X,Z}(D,z;\theta)) \\ =E_{Z \sim P(z|D;\theta^n)}(\sum_{t=1}^{N}\log P_{X,Z}(x_t,z_t;\theta)) \\ =\sum_{t=1}^{N} E_{Z \sim P(z|D;\theta^n)}(\log P_{X,Z}(x_t,z_t;\theta)) \\ =\sum_{t=1}^{N} E_{Z \sim P(z_t|x_t;\theta^n)}(\log P_{X,Z}(x_t,z_t;\theta))$